|
TIME
LAPSE AND HIGH SPEED NOTES
Andrew Davidhazy ROCHESTER INSTITUTE OF TECHNOLOGY If we take two photographs two days apart of the same general area and then we put them side by side, we are able to see the change that took place in the subject in two days. But we can't tell when and/or how the changes took place. By increasing the number of photographs, we can better estimate what actually happened between picture one and two, For example, if we take a photograph of a ball on the edge of a table, then we push it over the edge and make another exposure after it has fallen and stopped bouncing, we can infer by looking at these pictures that the ball moved from the table to the floor. We do not know when or how this happened. We need to take one or more photographs between picture one and two to fill in this lack of information. Although shooting at random would eventually provide the necessary information, a series of photographs at known time intervals will do it more quickly. The rate at which these have to be taken is governed by the requirement that no important part of the action should be missing. To accomplish this we can use a motion picture camera. This kind of camera makes discrete exposures at a frequency usually variable between 12 and 64 pictures per second. It is important to keep in mind that if we intend to project the photographs at 24 pps then a taking frequency rate of 24 pps will yield, on the screen, motion and time which takes place in as much time as it did in real life. That is, Screening time is related to real time as the frequency at which the photographs are taken divided by the rate at which they are shown. In this example the relationship is: 24 / 24 = 1X If we photograph events at less than 24 pps then we get a TIME REDUCTION or fractional TIME MAGNIFICATION as we look at the finished film. At 4 pictures per second we get a time magnification of 4 / 24 = 1/6X or a reduction of 6x. As we view the film on the projection screen we have reduced the time it takes an event to happen by a factor of 6. That is 6 second event in real time is shown in 1 second screen time. We are in the area of TIME LAPSE photography, although this range is more commonly associated with frequency rates of one picture every second or more. On the other hand, the photography of events at a frequency greater than 24 pps yields what is commonly known as TIME MAGNIFICATION. At a rate of 64 pps we get: Frequency of Photography / Frequency of projection = 64 / 24 = 2.66X The real time of the event has been expanded on the screen by a factor of 2.66. A one second real event takes 2.66 of screen time. We are in the range of HIGH SPEED MOTION PICTURE PHOTOGRAPHY, although this area is more commonly associated with frequencies over 120 pictures per second. How to determine time between photos in Time Lapse applications? By way of quick review on time lapse, it is helpful to remember that in most situations it is easier to compute the interval between frames by keeping in mind the total time of the event in seconds and the number of frames available or required to do the job. For example, let's say we want to photograph the way a sunflower "follows" the sun as it appears to move through the sky. We are concerned with a total event time of about 12 hours. In seconds that is 12h x 60 m/hr x 60 sec/min or 3600 x 12 = 43,200 sec Assume we will use 16m x 100 ft. film which is 4000 frames or 40 frames per foot. If we approach this from the digital point of view then we determine how many “frames” we can store on the camera's memory card. For the sake of simplicity we will assume it can hold 4000 frames – like the 100 ft of 16 mm film! Allow 10 feet to shoot a 5 foot "lead in" and a 5 foot "exit" at normal (24 fps) speed at the beginning and end of the roll respectively. There are 90 feet left to do the recording. That is, 90 x 40 = 3,600 frames. In the digital realm we would allow 200 frames for the recording at a fast rate of a lead in sequence and allow another 200 frames for the exit sequence. That leaves us 3600 frames for capturing the 12 hour long event. We have “duplicated” the requirements discussed with the film based solution, Now total event time divided by total number of available frames is 43,200 sec. / 3,600 frames = 12 sec./frame. That is, 12 seconds must elapse between each exposure. To find out how long the time lapse sequence will take on the screen, divide 3,600 frames by 24 fps (in the case of film) and you get 150 seconds which is 2 ½ minutes. If these are projected at 30 frames per second (common with video projection) then the on-screen time drops to exactly minutes for the action of the sunflower. There are many methods by which a movie camera can be made to automatically take photographs at preset time intervals. The best, of course, is usually the use of a commercial device, an intervalometer. Lacking this, a motor with a cam can be adapted to do the job over a limited range of speeds. If no auxiliary equipment is available then one can always resort to manual firing of the camera at the preset time intervals. This can get rather monotonous for events of long duration but patience and perseverance will most probably yield very interesting and surprising results. In addition to simply firing the camera every so often sometimes ancillary devices such as lamps of a special quality or window shades or grow lamps, etc. need to be turned on or off during the recording process. This is particularly evident in cases where daylight is used as the source of illumination for the color quality of the light changes during the day as well as the onset of night needs to be deal with somehow. Keeping light on is one solution but this sometimes interferes with subject behavior. Below is a schematic of a 555 time IC based 4 stage intervalometer and a brief description of the function of each stage.  and this is the basic electrical schematic minus the relays and LEDs – just the 4 basic 555 timers set up in astable mode. 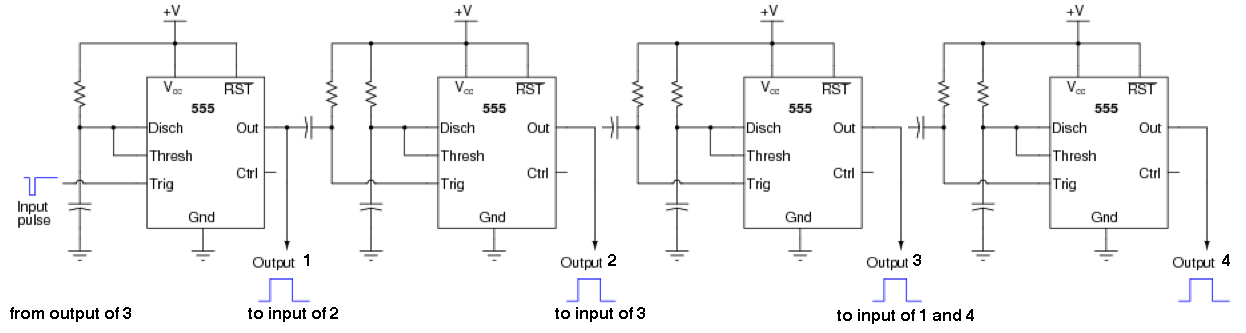 And what about high speed recording situations? Popular intermittent movement cameras which stop the film for each exposure (such as the Bolex, the Arriflex, Kodak Cine Special and similar models) usually can't go any faster than 64 pictures per second because of mechanical and physical limitations. There are, however, specialized intermittent and pin registered cameras that operate at up to 500 pps. These include the Locam, the Milliken and the PhotoSonics 1PL and others. Motion picture cameras that operate at high speeds usually do so by recording the subject onto moving film. This can be accomplished by using a very short exposure, so that the film does not move appreciably during exposure or by using a longer exposure but moving the image of the subject so that it remains stationary with respect to the film during the exposure. These cameras usually employ a rotating block of glass (a 2, 4, or 8 sided prism) to accomplish this. They include the Hycam and the Fastax cameras. Framing rates as high as 10,000 pps can be achieved by them on full frame 16 mm film. Using only a 1/2 height format this rate can be doubled and at 1/4 frame height the rate can be quadrupled. Thus, at 8,000 fps the TIME MAGNIFICATION or expansion produced is equal to 8,000 / 24 which is about 333X and a one second event would last almost 6 minutes on the screen assuming one has enough film to accommodate the 8,000 frames. In the case of digital high speed systems the operational characteristics vary but one always is concerned with the amount of data that can be recorded on the available storage device and how fast this space will be filled up by the data generated by the camera. Once one has reached the maximum data transfer process then, as in the case of film, making the images smaller and thus losing spatial resolution, allows for faster recording. It is a matter of compromises. A slightly different method, that of stroboscopic lighting, can be used successfully in many cases to obtain results similar to the ones which can be obtained with a film motion picture camera or a digital high speed camera. Usually stroboscopic lighting is used with cyclic events rather than random ones. That is, stroboscopes are more suited for investigating events that repeat themselves, such as rotating shafts, the action of cams and gears, etc. High speed cameras, on the other hand, are used to study random events such as explosions, fractures, fatigue in various materials, etc. With stroboscopic exposure or lighting one generally records on one piece of photosensitive material (film or electronic sensor) various positions of the subject. It is thus very suitable for the "instant" visualization of acceleration or speed changes because reference points remain fixed, Motion pictures contain the same information but each frame has to be measured and compared to previous ones which makes for more difficult analysis. Generally the main problem in high speed photography, however, is not how fast and at what rate we can take photographs but how the event is to be synchronized to the photography. At high framing rates, most cameras are only "available" for less than one or two seconds. Thus, the photography of random events is almost impossible. Either the camera or the event has to be made dependent on the other or both dependent on an independent timing network. Recent developments associated with digital high speed recording processes allow for the continuous recording of a process. Once the storage medium is filled up then older image data is deleted and replaced with the newest image data. This is done continuously in a “loop”. When a failure occurs the recording is terminated shortly afterward. Since the digital image data preceding the failure is stored and available for examination. Thus the events leading up to the process failure as well as those following it can be examined and analyzed. This was impossible film based systems because they are non-erasable, reusable, materials. Synchronization can be achieved by various means. Photoelectric cells, microphones, and sound actuated switches, physical contact between event and mechanical switch, etc., are all useful for one application or another. For example, to photograph the duration and behavior of a flash from a flashbulb, the following steps might be followed: 1. A good estimate of the flash duration is made by guess or by monitoring its output with a photocell and an oscilloscope. 2. The desired projection time is subjectively established. 3. At this point either TIME MAGNIFICATION, TM, is determined by dividing the former, 1, into the latter, 2, or the total number of frames of the event on the finished record is determined by multiplying the expected projection time by the frequency of projection. 4. Multiplying TM times the frequency of projection gives the framing rate at which the H.S. camera must run, Dividing the total number of frames that the event must cover in the finished film by the event time will also yield the speed at which the camera must run at the time the event takes place. The feasibility of running the camera at the above speed is then determined from system specifications. (Read the instruction manual!!) If possible then one proceeds. Let's assume the camera speed must be 8000 pps. 5. At this time one needs to consider whether the image storage capacity of the camera system is sufficient to store the full length of the event. If not then one needs to decide when to start the camera relative to the event or when to star the event relative to the camera in order to capture those parts off the event of main interest. Essentially one needs to devote time and effort to deal with camera and event synchronization. Let's assume that one decides to ignite the flash lamp after the first 200 frames of a full 8000 frame record have been expended of the available storage space. The lamp must ignite .025 seconds after the camera starts. 7. The problem of designing the proper delay system is then solved. Other factors, of course, are usually also important such as the delay of the flashbulb to respond to current going through it, the delay of any relay in the circuit, etc. All these are accounted for so that the flash starts to ignite after 200 frames have been used up by the camera. Of course a "wild" shooting is possible and framing rate can be established "after the fact" from timing light marks on the edge of the film or timing data provided by the high speed digital camera specification chart.. This is not practical when the duration of the event is equal to the available footage. Then careful preparation has to be made. 8. If using film then the timing marks on the edge provide actual recording rate at the time the event took place. To determine framing rate with timing light marks you will know that the lights turn on-off-on 120 times per second. Then it is a simple matter of counting the number of frames between timing marks on the film and multiply this by 120. T number of frames between marks times Timing Light Frequency equals framing rate expressed as pps or pictures per second. NOTE: These are “generic” notes associated with Time Lapse and High Speed recording. They are not extensive and all encompassing but hopefully serve as a guide or review of some basic principles associated with effective visualization of events that last a long time and also events that last a very short time. The purpose is to alter the time frame of these events so that the human eye/brain system can more easily comprehend how these processes develop and progress during their lifetime. If
you have any questions or feedback feel free to contact me by email at andpph@davidhazy.org
|