As the rockets fly upwards film, attached emulsion-out onto a rotating drum inside of a camera housing, is made to move downwards at approximately the expected velocity of the image of the rockets. The film is actually moving slower than the rockets themselves because the lens on the camera is operating at a magnification of less than unity.

A capping shutter is placed on the camera lens to prevent rewrite, or double exposure, of the film loaded onto the camera's 12 inch circumference drum. The shutter, responding to the rocket's lift-off, opens as the rocket leaves the launch pad and closes soon after the rocket passes by the line in space delimited by the projected exposing slit located just in front of the moving film within the camera.

Below you will find the results of two instances where the film did not quite match the speed that the image of the moving rockets produced across the exposing slit in the camera. Nevertheless, you will see how the rocket's velocity can be determined from such records basing the measurements on either one of two alternative methods.
 

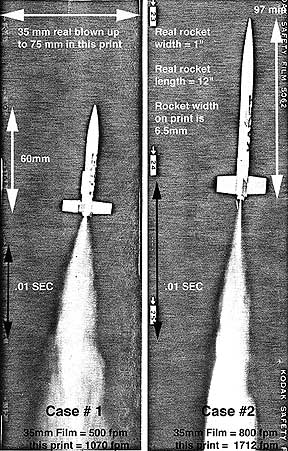
Aspect ratio based technique

Case #1 (image appears compressed)

The original negatives are enlarged in these example by a factor of 2.14x. This was determined by dividing the width of this print (about 75mm) by the width of the original 35mm negative namely 35mm.

The reference above is to the prints that served as the basis for this article. If you are reading this on the web the image sizes you are looking at may not match the print sizes. If this is so just imagine that you are looking at the prints at the alluded to size!

Given that the original film velocity through the camera was about 8.33 feet per second or 500 feet per minute we now analyze the resulting image to determine the actual speed of the rocket in this case fitted with a B6 engine.

Based on these facts if the original film was moving at 500 fpm and the negative was magnified 2.14x, the corrected film velocity for the image we are dealing with here is 500 fpm x 2.14 or 1070 fpm which is 1070 / 60 = 17.8 feet per second.

Now to determine the speed of the real rocket based on aspect ratio distortion we compare its proportions to those of the image recorded on film. The real rocket was 1n wide by 12n long or 1 to 12. This proportions of the image of the rocket in this record is 6.5mm by 60mm or about 1 to 9.2

Comparing the proportions of the real rocket to those of the photograph we find that the photograph shows the rocket to be slightly compressed and we can deduce from that that the film in the camera was traveling too slowly. In fact, compared to matching the speed of the image of the rocket the film was moving 12 / 9.2 or 1.3x as slowly as the image of the rocket was moving past the exposing slit in the camera.

From this we can conclude that the rocket's image was moving faster than the film. In fact it was moving 17.8 fpm x 1.3 or 23.2 fps.

To determine the speed that the real rocket was moving at we compensate for the magnification of the optics in the camera determined by simply comparing the width of the reproduced image of the rocket to that of the real rocket and divide the rocket's image speed by the magnification. In this case, the image speed is 23.2 fps which when divided by the magnification of the camera, (6.5 / 25.4) .256 results in a real rocket velocity of 90 feet per second.
 

Case #2 (image appears stretched)

In this case the rocket was fitted with a C engine and the film velocity was increased to 800 fpm or 13.33 fps.

The original negative was enlarged also by a factor of 2.14x and so the lvirtualn film velocity that we apply when working with this photograph is 13.33 x 2.14 or 28.5 fps.

The rocket was the same as for the first example and so the proportions of its width to length are 1 x 12. This record's width on the film is 6.5 mm as before but the length on the film is 97mm. So the proportions of the reproduction are 6.5 / 97 or 1 to 14.9.

Compared to the proportions of the real rocket the proportions of the reproduction indicate that the image is slightly stretched in comparison. This indicates the film was traveling too fast. In fact, it was traveling 14.9 / 12 or 1.24 times as fast as the image of the rocket was moving past the exposing slit in the camera.

From this we determine that the rocket's image was traveling 28.5 fps x 1.24 or 22.9 fps.

As before we now allow for the fact that the camera reduced (fractionally magnified) the real size of the real rocket and since the image on the original film is 6.5 mm while the width of the real rocket was 25.4 mm the operating magnification is 6.5 / 25.4 or .256 the real rocket was traveling 22.9 / .256 fps or 89.5 fps.

Conclusion

From these two tests we can deduce that regardless of the engine installed in the rocket it achieves a velocity of about 90 feet per second when about 8 feet off the launch pad. Presumably the difference between the two engines is the length of time during which the propellant burns.
 

Shortcut, subject size and image length based, Alternative Method:

Case #1

Knowing that the film in the camera was traveling at 500 fps or 8.33 feet/sec or 100 inches per second or 254 cm/sec one determines what the length of the rocket's image on the film is by direct measurement. 

In this case, since we are working with a 2.14 enlarged print from the negative, we measure the length of the rocket's image on this print and divide by the print magnification. On the print the rocket's image measures 60mm or 6 cm. This divided by a print magnification of 2.14 results in an image length on the original 35mm film of 2.8 cm. 

2.8 cm / 254 cm/sec indicates  that the rocket traveled its own length (from tip to tail-cone) in .011 sec. (or 1/90) seconds. Since the length of the real rocket was 1 foot  this indicates that it was traveling at 90 feet per second.

Case #2

In case two, the film was moving faster. At 800 feet per minute or 13.33 feet per second or 160 inches per second or 406 cm per second. The length of the rocket on the print is 97mm which needs to be  reduced by a factor of 2.14 to allow for the reduction of the image size from the original and this yields a length of the rocket on the original 35mm film of 45 mm or 4.5cm.

Therefore the rocket traveled its own length (1 foot) in 4.5cm / 406cm/sec or 1/90 second and thus the missile was moving at 90 feet per second.

Conclusion

Pretty good match between the two methods, don't you think?

If you have any questions about this material contact Prof. Andrew Davidhazy, Rochester Institute of Technology, 70 Lomb Memorial Drive, Rochester, NY 14623 (585) 475-2592 or send me email at andpph@rit.edu.